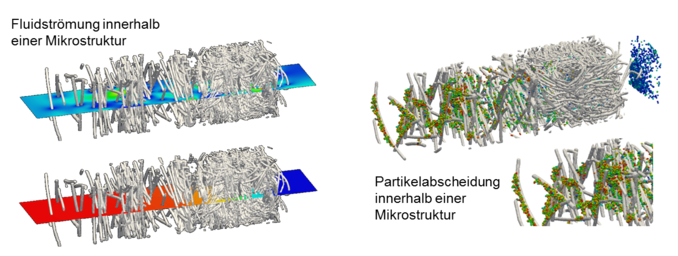
Simulation der Strömungsvorgänge und des Partikeltransports innerhalb von Mikrostrukturen
Die strömungsmechanischen Eigenschaften von Mikrostrukturen, wie etwa die Fitrationseffizienz von Filtermedien, werden maßgeblich durch ihren mikroskopischen Faseraufbau beeinflusst. Ausgehend von der geometrischen Erfassung solcher Mikrostrukturen, beispielsweise durch Computertomographie-Aufnahmen, können die Strömungsvorgänge innerhalb einer Mikrostrukturen mit modernen Lattice-Boltzmann Methoden berechnet werden. Mit speziell entwickelten numerischen Algorithmen lässt sich darüber hinaus der Transport von Partikeln und ihre Anlagerung an die mikroskopische Faserstruktur simulieren. Dabei werden alle relevanten Wechselwirkungen zwischen dem Fluid und den Partikeln, wie z.B. Widerstandskräfte und Brownsche Bewegung, berücksichtigt. Dies beinhaltet bei Anlagerungsprozessen insbesondere auch molekulare Kräfte, wie beispielsweise die van-der-Waals Kräfte. Die für die Durchströmung relevante Versperrung bereits abgeschiedener Partikel kann durch eine direkte Kopplung zwischen Partikel- und Fluidbewegung berücksichtigt werden.
Umfassende Berechnungen der Strömungsphänomene und des Partikeltransports innerhalb einer Mikrostruktur erlauben tiefe Einblicke in die physikalischen Vorgänge auf mikroskopischer Ebene und ermöglichen eine gezielte Optimierung der Geometrie solcher Faserstrukturen.
Numerische Verfahren
Für die Berechnung der strömungsmechanischen Phänomene innerhalb der Mikrostrukturen verwenden wir speziell entwickelte Lattice-Boltzmann Methoden (LBM). Ein großer Vorteil dieser Methoden besteht darin, selbst hochkomplexe Geometrien sehr einfach erfassen zu können. Die Berechnung der Partikelbewegung durch die Mikrostrukturen erfolgt durch explizite bzw. implizite Algorithmen zur Lösung der Bewegungsgleichungen der Partikel.
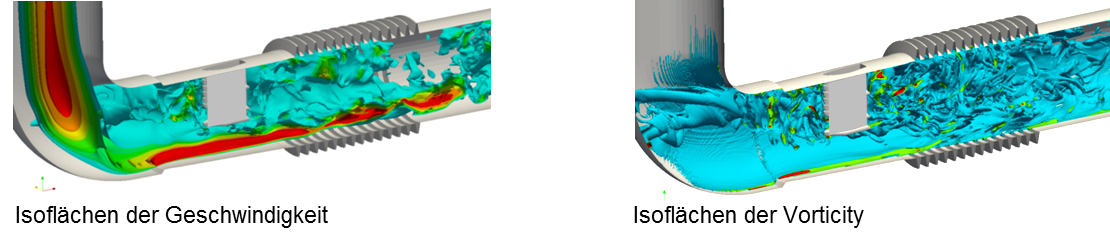
Large-Eddy-Simulationen (LES) turbulenter Strömungen
Im Vergleich zu den üblichen Reynolds gemittelten Navier-Stokes Strömungssimulationen (RANS) erlauben Large-Eddy Simulationen (LES) sehr detaillierte Einblicke in das räumliche und zeitliche Verhalten komplexer Turbulenzstrukturen.Dadurch erreichen solche Simulationen eine hohe Aussagequalität und bieten ausgezeichnete Optimierungsmöglichkeiten für die Entwicklung technischer Bauteile. Darüber hinaus ermöglichen insbesondere die zeitlichen Informationen über die turbulenten Vorgänge ganz neue Aussagen, die beispielsweise im Bereich der Aeroakustik von großem Interesse sind.
Numerische Verfahren
Für die Untersuchung turbulenter Strömungsvorgänge mit Large-Eddy Simulationen benutzen wir vorwiegend eigene numerische Verfahren, welche auf modernen Lattice-Boltzmann Methoden basieren.
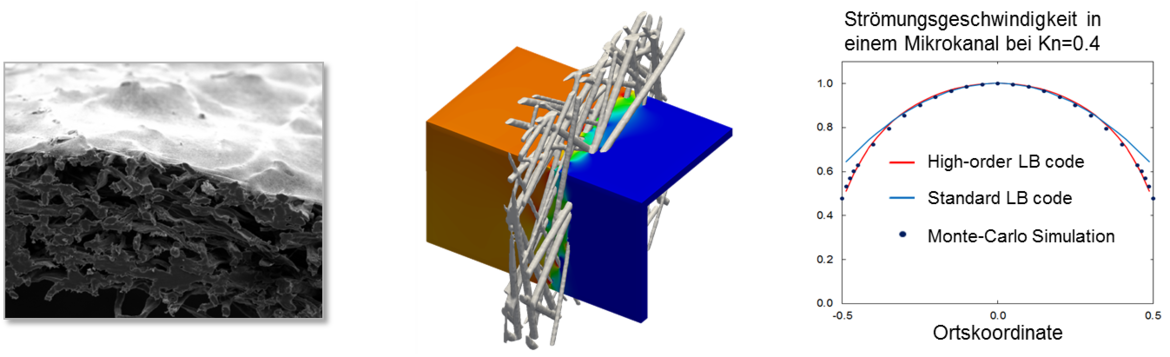
Lattice-Boltzmann Methoden hoher Ordnung zur Simulation von Strömungen bei endlichen Knudsen-Zahlen
Die Strömungsvorgänge innerhalb sehr kleiner geometrischer Strukturen beinhalten Strömungseffekte, welche nicht mehr durch Lösungen der Navier-Stokes Gleichungen darstellbar sind. Solche Fluidströmungen weisen starke Abweichungen vom thermodynamischen Gleichgewicht auf und sind durch eine endliche Knudsen-Zahl charakterisiert. Dabei ist die Knudsen-Zahl Kn durch das Verhältnis zwischen der mittleren freien Weglänge der Moleküle und einer typischen Längenskala des Strömungsproblems definiert.
Molekulardynamische Methoden bzw. Monte-Carlo Simulationen sind in der Lage diese Strömungsvorgänge mit zufriedenstellender Genauigkeit abzubilden. Allerdings ist der numerische Aufwand dieser Methoden so hoch, dass eine Anwendung für praktische Problemstellungen aufgrund der enormen Rechenzeiten in vielen Fällen problematisch ist.
Ein zentraler Vorteil von Lattice-Boltzmann Methoden mit hoher Ordnung besteht in der möglichen Erweiterung der Verfahren auf Strömungsphänomene jenseits des Gültigkeitsbereichs der Navier-Stokes Gleichungen. Diese Algorithmen sind in der Lage Strömungseffekte bei hohen Knudsen-Zahlen zu beschreiben und können somit starke Abweichungen vom thermodynamischen Gleichgewicht erfassen. Im Gegensatz zu den Monte-Carlo Methoden beinhalten diese Verfahren einen deutlich geringeren numerischen Aufwand und bieten sich daher insbesondere für die Anwendung auf industrielle Problemstellungen an.