Diese Seite enthält Studienarbeiten aus den Studiengängen Elektrotechnik und Informatik der Hochschule Aalen. Sie verwenden JavaScript.
Der „Zentrale Grenzwertsatz“ besagt, dass die Verteilung des Mittelwerts von n unabhängigen Zufallszahlen aus einer beliebigen Verteilung mit endlichem Mittelwert μ und endlicher Standardabweichung σ sich mit zunehmendem n immer mehr einer Normalverteilung mit Mittelwert μ und der Standardabweichung σ/√n annähert.
Mit diesem Applet können Sie beobachten,
- wie sich die Verteilung der mittleren Augenzahl von n Würfeln mit zunehmendem n immer mehr einer Normalverteilung annähert,
- wie die Breite dieser Normalverteilung mit zunehmendem n immer kleiner wird (der Mittelwert streut umso weniger, je größer der Stichprobenumfang ist),
- wie sich mit zunehmender Anzahl von Würfen die relative Häufigkeit der Würfelergebnisse immer mehr der berechneten Wahrscheinlichkeit annähert.
Der Zentrale Grenzwertsatz ist der Grund für die Bedeutung der Normalverteilung in der Statistik: Häufig ist man an der Verteilung von Mittelwerten interessiert, und auch die Zufallsstreuung eines Einzelwertes ist häufig die Summe vieler unabhängiger Einzelbeiträge und damit näherungsweise normalverteilt.
Dieses Applet stellt die Dichte der Binomial- und Poissonverteilung dar. Ziel des Applets ist es, zu zeigen,
- wie die Form der Verteilungsdichten von den jeweiligen Parametern abhängt,
- was ein Zufallsstreubereich ist.
Die Parameter der Verteilungen können eingegeben oder mit Schiebern verändert werden - das Applet zeigt dann die Form der Verteilungsdichte. Zusätzlich können Wertebereiche vorgegeben werden - das Applet hebt den gewählten Bereich dann grafisch hervor und berechnet die Wahrscheinlichkeit, mit der ein Ergebnis in diesem Bereich liegt.
Mit Hilfe dieses Applets kann der Anwender viele Stichproben aus der selben Grundgesamtheit erzeugen. Die Grundgesamtheit wird durch den Mittelwert und die Standardabweichung bestimmt. Der Umfang der Stichproben und deren Anzahl werden ebenfalls vom Anwender vorgegeben. Die grafischen Darstellungen sollen zeigen, dass
- die Stichprobenergebnisse streuen
- Mittelwerte weniger streuen als Einzelwerte
- die Verteilung der Einzelwerte, Mittelwerte, Varianzen und Standardabweichungen über viele Stichproben berechnet werden kann
- Mittelwert und Varianz erwartungstreue Schätzwerte sind, Varianz (1/n) und Standardabweichung aber nicht.
Das Wahrscheinlichkeitsnetz ist eine grafische Möglichkeit zu überprüfen, ob vorgegebene Daten zu einer angenommenen Verteilung passen oder nicht. Die Achsen werden so skaliert, dass die angenommene Verteilung als Gerade dargestellt wird.
Mit diesem Applet können eigene und simulierte Daten wahlweise in ein Wahrscheinlichkeitsnetz für normalverteilte, für logarithmisch normalverteilte und für weibullverteilte Merkmalswerte eingetragen werden. Zufallszahlen mit vorgegebener Verteilung können erzeugt und dargestellt werden. So können Sie beobachten, dass
- Daten aufgrund der Zufallsstreuung immer von der Geraden abweichen,
- diese Abweichungen aber mit zunehmendem Stichprobenumfang n immer kleiner werden, wenn die Stichprobe aus der jeweiligen Verteilung entnommen wurde,
- abweichende Verteilungen zu einer Abweichung von der Geraden führen,
- diese Abweichung bei kleinem Stichprobenumfang n aber nicht von der Zufallsstreuung unterscheidbar ist.
Für die Simulation kann als Verteilung auch eine beschnittene Normalverteilung (entsteht durch Aussortieren von Teilen außerhalb der Spezifikation) oder eine Mischverteilung (Teile von zwei unterschiedlichen Herstellern, Linien, Maschinen werden zusammengemischt) vorgegeben werden. So können Sie testen, ob solche typischen Abweichungen von einer Normalverteilung erkannt werden.
Visualisierung als JavaScript - bitte Chrome, Edge oder Firefox verwenden
Versuchsergebnisse, Messwerte usw. streuen aufgrund zufälliger Einflüsse. Daher unterliegen auch die aus mehreren Ergebnissen berechneten Mittelwerte und Standardabweichungen dem Zufall. Aus jeder Messreihe (Stichprobe) erhält man einen etwas anderen Mittelwert.
Doch wo liegt der wahre, leider normalerweise unbekannte Mittelwert der Grundgesamtheit (d.h. der Mittelwert, den man erhielte, wenn man den Versuch unter immer gleichen Bedingungen unendlich oft wiederholen könnte)? Der 95%-Vertrauensbereich (=Konfidenzbereich) für den Mittelwert ist ein Bereich, der bei durchschnittlich 95% der Stichproben den wahren Mittelwert der Grundgesamtheit enthält.
Das folgende Applet erzeugt fünfzig Stichproben mit einer frei wählbaren Anzahl (max. 9999) von Zufallszahlen. Die Einzelwerte der Stichproben stammen aus einer Normalverteilung, deren Mittelwert und Standardabweichung vorgegeben werden. Das Applet berechnet dann für jede Stichprobe Mittelwert und Standardabweichung dieser Stichprobe, sowie den 95%- und 99%-Vertrauensbereich für den Mittelwert. Alle Vertrauensbereiche werden grafisch dargestellt.
Bitte achten Sie auch auf folgende Punkte:
- Aus jeder Stichprobe erhält man einen anderen Vertrauensbereich, da Mittelwert und Standardabweichung der Stichprobe dem Zufall unterliegen.
- Durchschnittlich 95% der 95%-Vertrauensbereiche (bzw. 99% der 99%-Vertrauensbereiche) enthalten den wahren Mittelwert (das Maximum der Kurve).
- Die 99%-Vertrauensbereiche sind immer breiter als die 95%- Vertrauensbereiche.
- Je größer der Stichprobenumfang, desto schmäler sind die Vertrauensbereiche im Allgemeinen. Dennoch streut die Breite, weil Standardabweichung der Stichprobe streut.
Häufig sollen zwei Lieferchargen, Fertigungsverfahren, Prozess- oder Produktvarianten verglichen werden. Man möchte wissen, ob sich die wahren aber unbekannten Mittelwerte der beiden Gruppen (=Grundgesamtheiten) unterscheiden oder nicht. Dazu wird aus jeder Gruppe eine Stichprobe entnommen.
Die Differenz der Stichprobenmittelwerte ist ein Schätzwert für den wahren Unterschied der Mittelwerte der Grundgesamtheiten Δµ – sie unterliegt aber der Zufallsstreuung. Daher stellt sich die Frage: Unterscheiden sich die Mittelwerte der beiden Grundgesamtheiten wirklich oder ist der beobachtete Unterschied der Stichprobenmittelwerte nur auf die Zufallsstreuung zurückzuführen?
Im folgenden Applet wird unterstellt, dass Stichproben vom gleichen Umfang n (einstellbar im Bereich 2 bis 30) aus zwei Grundgesamtheiten gezogen werden, deren Mittelwerte sich um die wahre Differenz Δµ unterscheiden (einstellbar im Bereich von 0 bis 10). Die wahre Standardabweichung σ ist für beide Grundgesamtheiten gleich (einstellbar im Bereich 1 bis 3), ihr Wert ist dem Anwender aber normalerweise unbekannt.
Im Applet kann zwischen zwei Darstellungen umgeschaltet werden:
- Verteilungen enthält die Verteilung
- der Einzelwerte (blau, abschaltbar, Normalverteilung wird angenommen)
- die Verteilung der "Differenz der Mittelwerte", wenn Δμ=0 (zentriert um 0) und
- die Verteilung der "Differenz der Mittelwerte" für den vorgegebenen Wert für Δμ.
- Stichprobenergebnisse enthält die aus den Ergebnissen von je 20 Stichproben berechnete Differenz der Mittelwerte und 95%- und 99%-Vertrauensbereiche (=Konfidenzbereiche) für diese Differenz.
Vergleichen Sie die beiden Darstellungen und beobachten Sie interaktiv, wie sich die Veränderung der Parameter auswirkt. So erleben Sie den Mittelwertvergleich (=Zwei-Stichproben-t-Test) und verstehen nachher hoffentlich besser, worauf bei der Planung zu achten ist und was die Ergebnisse bedeuten.
Mit diesem Applet können Sie Punkte in ein Koordinatensystem einzeichnen und die zugehörige Regressionsgerade berechnen und darstellen lassen - oder Sie verwenden vorgegebene Beispiele als Ausgangspunkt. Zeichnen Sie eine Gerade von Hand ein und vergleichen Sie Ihre Gerade mit der Regressionsgeraden. Das Ziel ist, die Summe der quadrierten Abweichungen zu minimieren. Als Hilfe können Sie die quadratischen Abweichungen von der Geraden darstellen lassen. Lassen Sie den Vertrauensbereich für die Regressionsgerade und den Vorhersagebereich für Einzelwerte berechnen und beobachten Sie, wie sich die Bereiche unterscheiden und wie sie sich mit den Punkten verändern.
Berechnen Sie die Residuen und Kennzahlen wie Hebel und Cook-Distanz und erleben Sie, wie diese sich mit den Daten verändern. Und beobachten Sie die Zerlegung der Summe der quadrierten Abweichungen in einen Anteil QREGRESSION, den die Regressionsgerade erklärt, und die Reststreuung QREST. Zerlegen Sie QREST dann weiter in eine Abweichung des jeweiligen Mittelwerts QLACK OF FIT und reine Zufallsstreuung um den jeweiligen Mittelwert QPURE ERROR. Im Vergleich zu QREST wird auch PRESS berechnet und visualisiert - hier wird die Gerade immer ohne den jeweils betrachteten Punkt berechnet und somit die Prognosefähigkeit der Geraden geprüft.
Ziel von EVOP ist die kontinuierliche Verbesserung von Fertigungsprozessen. Als Beispiel wird hier ein Spritzgießprozess betrachtet.
Aufgabenbeschreibung:
Ein Kunststoff - Spritzgießprozess wurde an einer Pilotanlage entwickelt und anschließend auf die Produktionsanlage übertragen.
Ziel ist es, Teile mit
- möglichst geringem Verzug (höchstens 0,02 mm, optimal sind Werte < 0,01 mm) und
- möglichst hoher Schlagzähigkeit (mindestens 8 kJ/m², optimal sind Werte > 10 kJ/m²)
herzustellen.
Wichtige Prozessparameter sind die Einspritzgeschwindigkeit der Masse in die Form (und damit die Zeit für das Füllen der Form) und der Druck nach dem Füllen der Form (Nachdruck). In der Pilotanlage wurde ermittelt, dass folgende Werte zu geringem Verzug und hoher Schlagzähigkeit führen:
- Einspritzgeschwindigkeit: 30 bis 35 mm/sec
- Nachdruck: 300 bis 350 bar.
Beim Übertragen in die Fertigung stellen Sie fest, dass die Mindestforderungen für Verzug und Schlagzähigkeit knapp erreicht werden.
Sie könnten nun als Sollwerte die Spezifikationsmitten (Einspritzgeschwindigkeit 32,5 mm/sec undNachdruck 325 bar) festlegen und sich freuen, dass Sie einen gerade noch ausreichend guten Prozess haben. Oder Sie suchen nach Möglichkeiten, Ihren Prozess zu verbessern. Dann verändern Sie Einspritzgeschwindigkeit und Nachdruck systematisch im Rahmen der Spezifikation.
Sie beobachten, wie Verzug und Schlagzähigkeit sich mit den Prozessparametern verändern. Da Sieinnerhalb der Spezifikation bleiben, verändern sich die Zielgrößen natürlich auch nur geringfügig.Das bedeutet, dass Sie bei jeder Parameterkombination verkaufsfähige Produkte erhalten.
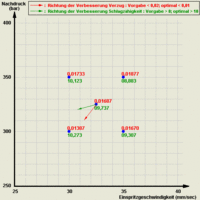
Aber natürlich ist Ihren Messwerten auch eine Zufallsstreuung überlagert (Messfehler, kleine, nicht kontrollierbare Veränderungen der Umgebungsbedingungen und diverser anderer Prozessparameter). Daher sollten Sie den Versuchsplan mehrmals durchlaufen bis Sie sich sicher sind, dass die Veränderungeines oder beider Prozessparameter in eine bestimmte Richtung wirklich eine Verbesserung bringt. Als Entscheidungshilfe wird der Effekt der Prozessparameter und die Breite des 95%-Vertrauensbereichesberechnet - wenn der Betrag eines Effektes größer ist als die Breite des Vertrauensbereiches, dann können Sie sich ziemlich sicher sein, dass der beobachtete Effekt echt ist und nicht nur zufällig. Man sagt, der Effekt ist statistisch signifikant. Signifikante Effekte sind rot gekennzeichnet und im 2D-Diagramm als Pfeil dargestellt.
Wenn Sie überzeugt sind, dass die Veränderung eines oder beider Prozessparameter in eine bestimmte Richtung zu einer Verbesserung der Zielgröße(n) führen, dann verändern Sie die Spezifikation vorsichtig in diese Richtung und beobachten den Prozess erneut.
Wiederholen Sie den Vorgang und beobachten Sie, wie Sie immer besser werden - bis Ihnen das Ergebnis gut genug istoder bis keine weitere Verbesserung mehr möglich ist. Sie haben dann erlebt, wie Sie durch vorsichtige Veränderung der Prozessparameter während der laufenden Fertigung nicht nur Ihr Produkt herstellen können, sondern auch Wissen über Verbesserungsmöglichkeiten erhalten. So können Sie immer besser werden.