Neues Papier löst Beck's Problem auf sternförmigen GraphenGruppe im Research Center for Complex Systems liefert den ersten Beweis dafür, dass Lösungen von Beck's Problem auf Sterngraphen exponentiell stabil sind
Wenn die Professoren vom Research Center for Complex Systems versuchen, mathematische Probleme zu lösen, fragen sie, in welchem abstrakten Rahmen die Probleme behandelt werden können und wie dieser abstrakte Rahmen erweitert werden muss. Um Fragestellungen aus der unendlich-dimensionalen Systemtheorie zu beantworten, beschäftigt sich die Gruppe von Prof. Dr. Mahyar Mahinzaeim u. a. mit Anfangsrandwertproblemen für partielle Differenzialgleichungen. Dafür bildet die Theorie der stark stetigen Halbgruppen und ihrer infinitesimalen Erzeuger einen solchen abstrakten Rahmen. Zusammen mit internationalen Partnern von der Tianjin University hat Mahinzaeim kürzlich einen Artikel veröffentlicht, in dem die bisher ungelöste Frage beantwortet wird, ob Beck's Problem auf einem Sterngraphen exponentiell stabil ist. Dafür wurde die exponentielle Stabilität der zugehörigen Halbgruppe untersucht.
"Beck's Problem ist ein mittlerweile klassisches Problem im Bereich der elastischen Stabilität. Es wurde im Jahr 1952 in einem Artikel in der Zeitschrift für angewandte Mathematik und Physik ZAMP gestellt und befasst sich mit der Stabilität der Lösung eines linearen nichtkonservativen Anfangsrandwertproblems vierter Ordnung in Abhängigkeit von einem Parameter, nennen wir ihn p", sagt Mahinzaeim. "Physikalisch handelt es sich dabei um das Problem des Stabilitätsnachweises bei einem Stab unter axialer Folgekraft proportional zu p."
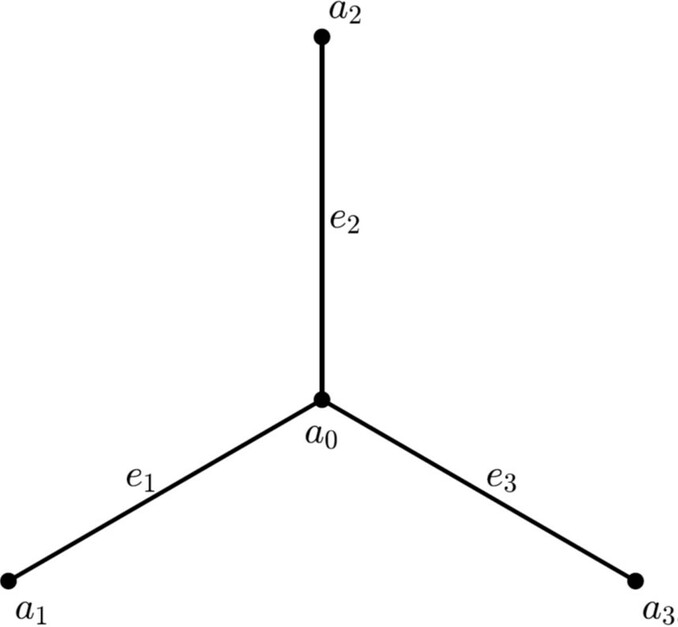
Trotz seiner langen Existenz in der Ingenieursliteratur hat Beck's Problem erst in den vergangenen Jahrzehnten in der Mathematik Beachtung gefunden, zunächst in seiner Original-Formulierung für den Fall eines einzigen Stabes. Frühere Ansätze bestimmten den kritischen Parameter p, d.h. die kritische Kraft, die erforderlich ist, um Instabilitäten herbeizuführen, mittels Eigenwertanalyse. Dieses Vorgehen ist bei Anfangsrandwertproblemen für partielle Differentialgleichungen aber nicht ohne Weiteres anwendbar. "Bei linearen Anfangswertproblemen für gewöhnliche Differentialgleichungen bestimmen die Eigenwerte, von denen es nur endlich viele gibt, vollständig die Stabilität der Lösungen: die Lösungen sind exponentiell stabil, wenn alle Eigenwerte in der offenen linken Halbebene liegen, also negative Realteile haben. Das Spektrum eines partiellen Differentialoperators kann Elemente enthalten, die keine Eigenwerte sind. Darüber hinaus ist es möglich, dass das Spektrum in der offenen linken Halbebene enthalten ist und Lösungen des Anfangsrandwertproblems möglicherweise nicht einmal asymptotisch, geschweige denn exponentiell stabil sind", erklärt Mahinzaeim. Die Forschungen von Mahinzaeim und seinen Partnern setzen hier an und fragen danach, wie und unter welchen Bedingungen die exponentielle Stabilität der zugehörigen Halbgruppe allein anhand des Spektrums des infinitesimalen Erzeugers abgeleitet werden kann. Ihre Arbeit befasst sich dabei mit der Abbildung von Beck’s Problem als Sterngraph mit drei identischen, endlich langen Kanten und Dämpfung im Sternzentrum und liefert den analytischen Beweis, dass für p beliebig aber positiv exponentielle Stabilität vorliegt.
Ihr theoretisches Ergebnis könnte Physikerinnen und Physikern sowie Ingenieurinnen und Ingenieuren beispielsweise bei der Analyse von Wellenvorgängen in Netzwerken helfen. "On the exponential stability of Beck's Problem on a star-shaped graph", veröffentlicht im Journal of Differential Equations, ist hier verfügbar.
Die Forschung wurde teilweise vom National Natural Science Foundation of China unterstützt.